Discussion of factors affecting accuracy of the model

 
The clear sky solar radiation model calculates solar radiation at the Earth's surface based on solar radiation at the top of the atmosphere (extraterrestrial radiation) and empirical extinction coefficients for direct beam and diffuse radiation components. The extinction coefficients are calculated from empirically-derived equations that account for the physical factors that govern radiative transfer through the atmosphere, such as atmospheric composition and air mass. Extraterrestrial radiation is based on a theoretical calculation from the solar constant, and accounts for day of year, time of day, latitude, and longitude. These factors determine the position of the sun relative to the measurement site, and thus the solar radiation at the top of the atmosphere magnitude for the given site.

Based on comparison to solar radiation measurements from multiple sites representing a wide range of conditions, the accuracy of the clear sky radiation model can be +/- 3 % if the calculation is made in the summer, near solar noon, and on a cloudless, non-polluted day (Rick Allen, personal communication). Achieving this accuracy requires that all of the inputs are measured or estimated accurately (air temperature, relative humidity, day of year, time of day, elevation, latitude, and longitude).
 

Good accuracy also requires completely clean air. An additional source of error is atmospheric haze caused by particulate matter and aerosols in the air. Haze can reduce the incident radiation at solar noon by 6% and in some instances by as much as 10%. In some locations, haze is common during the summer months and is usually visually apparent. The presence of haze causes sensors to read lower than the model estimate, resulting in a false impression of downward sensor drift. If you live in a location with haze it is particularly important to compare readings over multiple days. In these locations, the best time to make a comparison is a clear day shortly after a rainfall event when the rain washes the particulate matter out of the air.

When the model is run at solar noon, the figures below show the effect of each input parameter on model output. Relative humidity and temperature (figures 1 and 3) have the largest effect on model output.
 

 
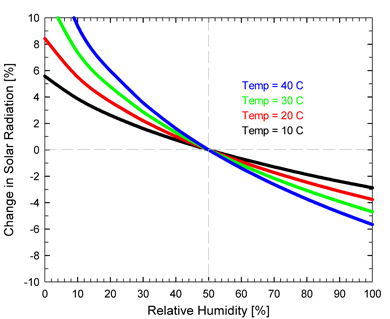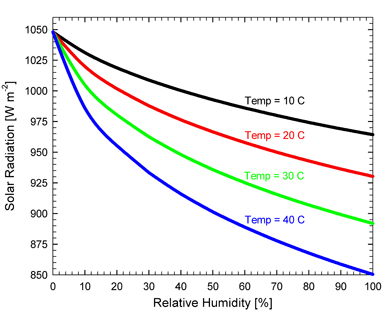
Figure 1:      Clear sky solar radiation [W m-2] calculated from the model (y-axis) as a function of relative humidity (RH) [%] (x-axis) at 10, 20, 30, 40 C. Radiation decreases with increasing humidity due to increasing attenuation by water vapor molecules. For example, at 30 C and 50 % RH, radiation is 935 W m-2.

If RH decreased to 40 %, radiation would increase about 1.5% to 950 W m-2. If RH increased to 60 %, radiation would decrease about 1% to 925 W m-2.

 
Figure 2:      Clear sky solar radiation error [%] (relative to clear sky solar radiation at the relative humidity (RH) of the measurement site) (y-axis) as a function of the RH [%] (x-axis) at 10, 20, 30, 40 C air temperature (it is assumed site RH is 50 %). Radiation decreases with increasing humidity due to increasing attenuation by water vapor molecules. For example, at 30 C if estimated RH was 10 % lower or higher than actual RH, the error in clear sky solar radiation is approximately +1 and -1 %, respectively. As the air temperature increases, the error in clear sky solar radiation increases.

 
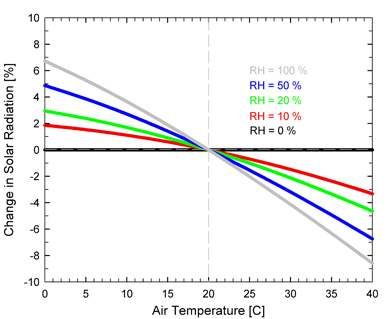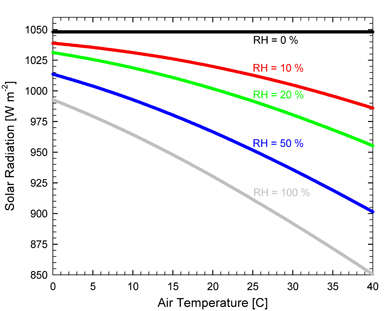
Figure 3:      Clear sky solar radiation [W m-2] calculated from the model (y-axis) as a function of air temperature [C] (x-axis) at 0, 10, 20, 50, 100 % relative humidity. Radiation decreases with increasing temperature due to increasing attenuation by water vapor molecules (even though humidity is constant, at higher temperature, the air has a greater capacity to hold water vapor).

For example, at 20 % RH and 20 C, radiation is 1000 W m-2. If air temperature decreased to 15 C, radiation would increase 1% to 1010 W m-2, and if air temperature increased to 25 C, radiation would decrease 1% to 990 W m-2.

 
Figure 4:      Clear sky solar radiation error [%] (relative to clear sky solar radiation at the air temperature of the measurement site) (y-axis) as a function of the air temperature [C] (x-axis) at 0, 10, 20, 50, 100 % relative humidity (it is assumed site air temperature is 20 C). Radiation decreases with increasing temperature due to increasing attenuation by water vapor molecules (even though humidity is constant, at higher temperature, the air has a greater capacity to hold water vapor).

For example, at 20 % RH if estimated air temperature was 5 C lower or higher than actual air temperature, the error in clear sky solar radiation is approximately +1 and -1 %, respectively. As the RH increases, the error in clear sky solar radiation increases.


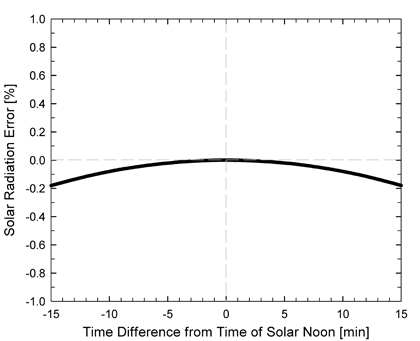Figure 5:      Clear sky solar radiation error [%] (relative to clear sky solar radiation at solar noon) (y-axis) as a function of the time difference from solar noon (x-axis). The plot shows the error in the clear sky solar radiation calculation if there is an error in the time measurement input into the model. For example, if the clock used to measure time was 10 minutes behind actual time (-10) or 10 minutes ahead of actual time (+10), the error in clear sky solar radiation is approximately -0.1 %.


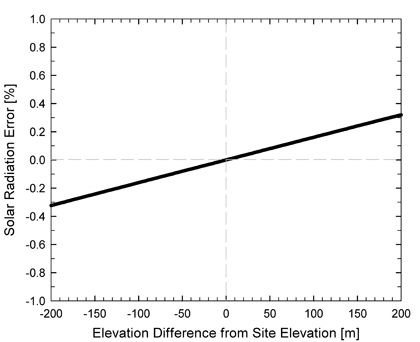Figure 6:      Clear sky solar radiation error [%] (relative to clear sky solar radiation at the elevation of the measurement site) (y-axis) as a function of the elevation difference from measurement site elevation (x-axis). The plot shows the error in the clear sky solar radiation calculation if there is an error in the elevation measurement/estimate input into the model. For example, if the elevation is 100 meters lower (-100) or 100 meters higher (+100) than the actual measurement site elevation, the error in clear sky solar radiation is approximately -0.15 and +0.15 %, respectively.


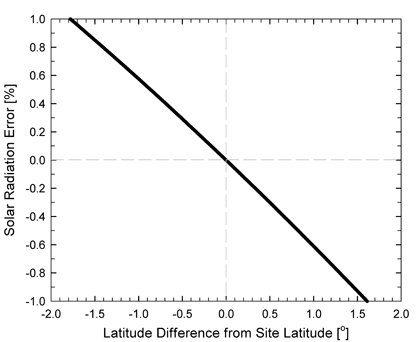Figure 7:      Clear sky solar radiation error [%] (relative to clear sky solar radiation at the latitude of the measurement site) (y-axis) as a function of the latitude difference from measurement site latitude (x-axis). The plot shows the error in the clear sky solar radiation calculation if there is an error in the latitude measurement/estimate input into the model. For example, if the latitude is 1 degree less (-1) or 1 degree greater (+1) than the actual measurement site latitude, the error in clear sky solar radiation is approximately +0.6 and -0.6 %, respectively.


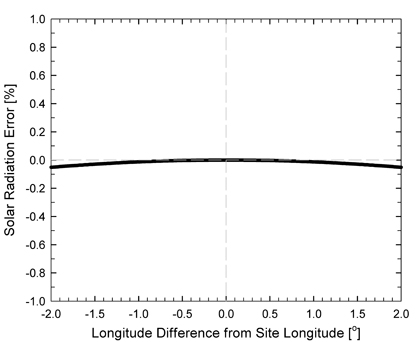Figure 8:        Clear sky solar radiation error [%] (relative to clear sky solar radiation at the longitude of the measurement site) (y-axis) as a function of the longitude difference from measurement site longitude (x-axis). The plot shows the error in the clear sky solar radiation calculation if there is an error in the longitude measurement/estimate input into the model. For example, if the longitude is 1 degree less (-1) or 1 degree greater (+1) than the actual measurement site longitude, the error in clear sky solar radiation is approximately -0.05 %.

All the data shown in the graphs are for solar noon on the summer solstice. For measurements made near solar noon (within an hour) in the summer months, small errors in time (+/- 10 minutes), elevation (+/- 100 meters), latitude (+/- 1 degree), and longitude (+/- 1 degree) have a negligible (less than 1 %) effect on the prediction of clear sky solar radiation from the model. However, errors in the measurement/estimate of air temperature and relative humidity have a much larger effect, as evidenced by the steep slopes of the lines in Figures A and B.

Errors caused by comparing over different time intervals. Another source of error is caused by the time averaging function that is commonly used in data acquisition systems. Many users average their radiation data over a one hour time interval. The model calculates radiation at a single moment in time. The average value from the datalogger is typically associated with the time at the end of the interval (at noon the datalogger would output an average value from measurements made over the previous 60 minutes). If the interval is prior to solar noon, the datalogger will output a value lower than the model value. If the time interval is after solar noon the datalogger would output a value higher than the model. Please check the time average function in your datalogger and consider this source of error in your comparison. This error can be minimized if the time interval includes 30 minutes before and after solar noon. If the interval includes solar noon the error is less than 1 %. Comparing measurements made just shortly and shortly after solar noon can also be used to minimize this error.
 

Discussion of accuracy of the calculation of photosynthetic photon flux from total shortwave radiation

The clear sky solar radiation model can be used to estimate the clear sky photosynthetic photon flux (PPF). Conversion of the value for total shortwave radiation to PPF requires the following two factors:

1. The weighted average energy content of photosynthetic photons (400-700 nm)
2. The ratio of the energy in photosynthetic radiation (400-700 nm) to total solar radiation.

The energy content of the photons is determined from Planck's equation (E = hc/lambda). The average wavelength between 400 and 700 nm is often taken as 550 nm, which results in an energy content of 217.5 kJ per mole of photons. We used a spectroradiometer to determine the radiation at 1 nm intervals from 400 to 700 nm at solar noon in the summer months. The energy content of the photons was 218 kJ per mole.

The ratio of photosynthetic to total radiation is approximately 0.45. Meek et al. (1984) measured this ratio at multiple sites in the western United States and found the mean value was 0.45 � 0.01 on a daily total basis. Weiss and Norman (1985) confirmed the fractional values of Meek et al. in a subsequent study. Their measurements give a mean value of 0.46 for what they call "a range of sky conditions". The value changed very little over a range of zenith angles until the zenith angle was about 80 degrees. They cite multiple studies, including Meek et al. (1984), and the range appears to be 0.45-0.50 for studies outside of the tropics. Four of the papers they cite give a mean value of 0.45 or 0.46. The effect of changes in this ratio on clear sky PPF are shown in the adjacent figure.

 
Figure: The effect of changes in the fraction of photosynthetically active radiation (PAR) on the calculation of the clear sky photosynthetic photon flux (PPF, umol m-2 s-1). The model assumes a constant fraction of 0.45, but the calculated value of PPF changes up to 4% depending on the exact ratio. Meek et al. (1984) found that this ratio was 0.45 +/- 0.01 across a range of latitudes, elevations, and climates.

 
References:

Meek, D.W., J.L. Hatfield, T.A. Howell, S.B. Idso, and R.J. Reginato, 1984. A generalized relationship between photosynthetically active radiation and solar radiation. Agronomy Journal 76:939-945.

Weiss, A., and J.M. Norman, 1985. Partitioning solar radiation into direct and diffuse, visible and near-infrared components. Agricultural and Forest Meteorology 34:205-213.